Image segmentation is the basis and premise of image processing, though traditional multi-threshold image segmentation methods are simple and effective, they suffer the problems of low accuracy and slow convergence rate. For that reason, this paper introduces the multi-threshold image segmentation scheme by combining the harmony search (HS) optimization algorithm and the maximum between-class variance (Otsu) to solve them. Firstly, to further improve the performance of the basic HS, an ameliorated harmony search (AHS) is put forward by modifying the generation method of the new harmony improvisation and introducing a convergence coefficient. Secondly, the AHS algorithm, which takes the maximum between-class variance as its objective function, namely AHS-Otsu, is applied to image multi-level threshold segmentation. Finally, six test images are selected to verify the multilevel segmentation performance of AHS-Otsu. Peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) are two commonly used metrics for evaluating the effectiveness of image segmentation, which are both used in this article. Comprehensive experimental results indicate that the AHS-Otsu does not only has fast segmentation processing speed, but also can obtain more accurate segmentation performance than others, which prove the effectiveness and potential of the AHS-Otsu algorithm in the field of image segmentation especially for the multi-threshold.
| Published in | Automation, Control and Intelligent Systems (Volume 12, Issue 3) |
| DOI | 10.11648/j.acis.20241203.12 |
| Page(s) | 60-70 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Image Segmentation, Harmony Search, Otsu, Multi-threshold
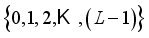 . If the image is considered to be divided into m regions, so (m-1) appropriate thresholds should be chosen to partition the solution space.
. If the image is considered to be divided into m regions, so (m-1) appropriate thresholds should be chosen to partition the solution space. 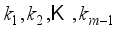 , then the distribution of the multiple segmentation regions obtained is:
, then the distribution of the multiple segmentation regions obtained is: 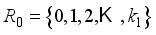 ,
, 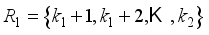 ,...,
,..., 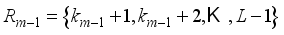 .
. 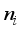 , so the amount of pixels in the whole image is
, so the amount of pixels in the whole image is 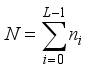 . Meanwhile, the proportion of the pixel with level i is
. Meanwhile, the proportion of the pixel with level i is 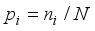 . Then the percentage of pixels in each partition of the image can be calculated as:
. Then the percentage of pixels in each partition of the image can be calculated as: 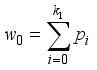 ,
, 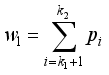 , …,
, …, 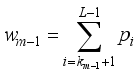 .
. 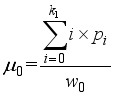 ,
, 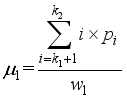 ,…,
,…, 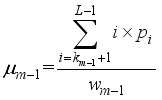 , and the whole mean value of the image is
, and the whole mean value of the image is 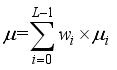 .
. 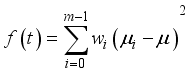 (1)
(1) 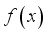 which needs to be maximized (or minimized), and x is a candidate solution consisting of
which needs to be maximized (or minimized), and x is a candidate solution consisting of 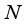 decision variables
decision variables 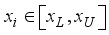 ,
, 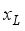 and
and 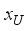 are the limiting boundaries. The initialization parameter settings include HMS, HMCR, PAR, bw and NI. All the above parameters are set manually.
are the limiting boundaries. The initialization parameter settings include HMS, HMCR, PAR, bw and NI. All the above parameters are set manually. 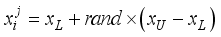 , in which the value of j is from 1 to HMS and
, in which the value of j is from 1 to HMS and 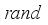 is a random number between 0 and 1. These harmony vectors are stored in HM.
is a random number between 0 and 1. These harmony vectors are stored in HM. 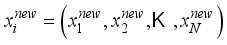 , which is obtained under the collaboration of parameters HMCR, PAR and bw. If operation meets the condition of HMCR, the new decision variables will be obtained based on the vectors that stored in HM, otherwise they are got by randomly selecting from the whole dataset. When operating under HMCR, if the value of judgement is less than PAR, the parameter bw will be used for the
, which is obtained under the collaboration of parameters HMCR, PAR and bw. If operation meets the condition of HMCR, the new decision variables will be obtained based on the vectors that stored in HM, otherwise they are got by randomly selecting from the whole dataset. When operating under HMCR, if the value of judgement is less than PAR, the parameter bw will be used for the 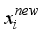 , i.e.
, i.e. 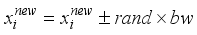 .
. 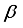 will be expressed as:
will be expressed as: 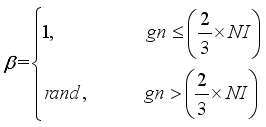 (2)
(2) 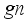 is the current generation number and
is the current generation number and 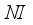 is the maximum iterations, and
is the maximum iterations, and 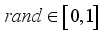 .
. 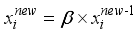 (3)
(3) 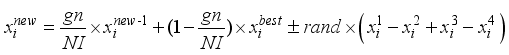 (4)
(4) 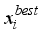 is the i-th variable in the current optimal vector,
is the i-th variable in the current optimal vector, 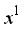 ,
, 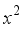 ,
, 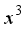 ,
, 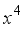 are the different harmony vectors randomly chosen from the HM.
are the different harmony vectors randomly chosen from the HM. 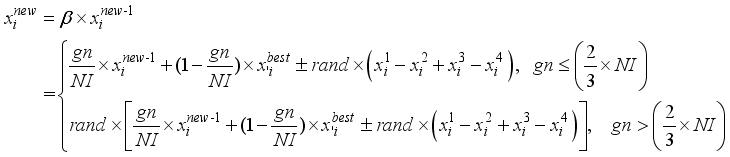 (5)
(5) 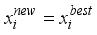 (6)
(6) 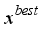 is the best performing harmony vector which stored in HM.
is the best performing harmony vector which stored in HM. 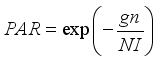 (7)
(7) 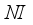 is the maximum value of iterations;
is the maximum value of iterations; 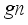 is the current generation number. The numerical variation curve of PAR is shown in Figure 1.
is the current generation number. The numerical variation curve of PAR is shown in Figure 1. 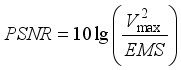 (8)
(8) 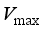 indicates the maximum grayscale value of the image; EMS imply the mean square error, that is:
indicates the maximum grayscale value of the image; EMS imply the mean square error, that is: 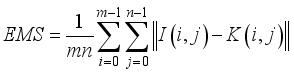 (9)
(9) 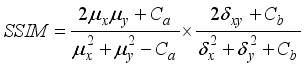 (10)
(10) 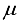 represents the brightness;
represents the brightness; 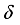 indicates the contrast of the image; Ca and Cb are two constants.
indicates the contrast of the image; Ca and Cb are two constants. Image | m= 2 | m= 3 | m= 4 | m=5 | |||||
|---|---|---|---|---|---|---|---|---|---|
Otsu | AHS-Otsu | Otsu | AHS-Otsu | Otsu | AHS-Otsu | Otsu | AHS-Otsu | ||
I1 | Time (s) | 0.016 | 0.098 | 0.236 | 0.102 | 6.306 | 0.111 | 672.406 | 0.114 |
PSNR | 8.468 | 8.468 | 12.660 | 12.660 | 15.313 | 15.313 | 32.519 | 32.519 | |
I2 | Time (s) | 0.015 | 0.087 | 0.245 | 0.097 | 6.210 | 0.105 | 694.827 | 0.108 |
PSNR | 8.315 | 8.315 | 16.003 | 16.003 | 18.468 | 18.468 | 34.814 | 34.814 | |
I3 | Time (s) | 0.014 | 0.095 | 0.239 | 0.114 | 7.188 | 0.117 | 618.147 | 0.117 |
PSNR | 8.167 | 8.167 | 14.050 | 14.050 | 15.882 | 15.882 | 32.823 | 32.823 | |
I4 | Time (s) | 0.017 | 0.095 | 0.222 | 0.096 | 5.347 | 0.094 | 673.506 | 0.113 |
PSNR | 9.836 | 9.836 | 11.531 | 11.531 | 17.928 | 17.928 | 34.034 | 34.034 | |
I5 | Time (s) | 0.017 | 0.091 | 0.221 | 0.093 | 5.291 | 0.109 | 642.521 | 0.111 |
PSNR | 6.812 | 6.812 | 16.596 | 16.596 | 20.495 | 20.495 | 35.428 | 35.428 | |
I6 | Time (s) | 0.014 | 0.088 | 0.238 | 0.093 | 5.435 | 0.096 | 696.203 | 0.106 |
PSNR | 9.937 | 9.937 | 12.626 | 12.626 | 16.441 | 16.441 | 36.069 | 36.069 | |
Image | Region | HS-Otsu | IHS-Otsu | GHS-Otsu | HHS-Otsu | PAHS-3-Otsu | IGHS-Otsu | AHS-Otsu |
|---|---|---|---|---|---|---|---|---|
I1 | 3 | 23.9339 | 23.9098 | 23.8775 | 23.9417 | 23.883 | 23.9421 | 23.9421 |
4 | 26.2078 | 26.2287 | 26.276 | 26.3004 | 26.2566 | 26.3058 | 26.3081 | |
5 | 27.6763 | 27.6078 | 27.5073 | 27.719 | 27.3715 | 27.7361 | 27.8095 | |
I2 | 3 | 22.0047 | 22.017 | 21.843 | 21.9811 | 22.0047 | 21.9811 | 22.0345 |
4 | 26.1539 | 26.228 | 26.2588 | 26.2628 | 26.1845 | 26.1678 | 26.2666 | |
5 | 28.0522 | 27.9551 | 27.7729 | 28.5355 | 28.1322 | 28.4981 | 28.5377 | |
I3 | 3 | 23.4997 | 23.4036 | 23.4738 | 23.5012 | 23.4998 | 23.5012 | 23.5012 |
4 | 26.0903 | 26.0988 | 26.1151 | 26.1217 | 25.8098 | 26.1111 | 26.1227 | |
5 | 27.4931 | 27.6748 | 27.8609 | 28.0167 | 27.6853 | 27.9888 | 28.0188 | |
I4 | 3 | 22.9618 | 22.97 | 22.909 | 22.9805 | 22.9444 | 22.9673 | 22.9805 |
4 | 24.8484 | 24.5768 | 24.9138 | 24.5357 | 24.9103 | 24.8004 | 24.9316 | |
5 | 26.5602 | 26.4402 | 26.6048 | 26.6168 | 26.176 | 26.6585 | 26.6747 | |
I5 | 3 | 23.2634 | 23.2668 | 23.2693 | 23.2796 | 23.2798 | 23.2798 | 23.2798 |
4 | 25.6289 | 25.6071 | 25.5851 | 25.666 | 25.6245 | 25.5415 | 25.6624 | |
5 | 27.6564 | 27.5769 | 27.4263 | 27.6878 | 27.437 | 27.3267 | 27.7061 | |
I6 | 3 | 22.6691 | 22.6691 | 22.6749 | 22.6781 | 22.6727 | 22.6781 | 22.6781 |
4 | 24.6835 | 24.7637 | 24.7485 | 24.8447 | 24.819 | 24.5947 | 24.7562 | |
5 | 26.7793 | 26.7025 | 26.1221 | 26.8527 | 26.5785 | 26.8379 | 26.8666 |
Image | Region | HS-Otsu | IHS-Otsu | GHS-Otsu | HHS-Otsu | PAHS-3-Otsu | IGHS-Otsu | AHS-Otsu |
|---|---|---|---|---|---|---|---|---|
I1 | 3 | 0.6619 | 0.6584 | 0.6721 | 0.6565 | 0.6368 | 0.6537 | 0.6537 |
4 | 0.721 | 0.7405 | 0.7281 | 0.7356 | 0.7335 | 0.7317 | 0.7337 | |
5 | 0.7698 | 0.7862 | 0.7461 | 0.7711 | 0.7754 | 0.7755 | 0.7872 | |
I2 | 3 | 0.5884 | 0.5861 | 0.5904 | 0.5878 | 0.5884 | 0.5878 | 0.5898 |
4 | 0.8307 | 0.8336 | 0.8268 | 0.8263 | 0.8249 | 0.8195 | 0.8289 | |
5 | 0.8526 | 0.8571 | 0.8611 | 0.8764 | 0.8583 | 0.8749 | 0.8755 | |
I3 | 3 | 0.7125 | 0.704 | 0.7116 | 0.7129 | 0.7124 | 0.7129 | 0.7129 |
4 | 0.7803 | 0.78 | 0.7837 | 0.7796 | 0.7806 | 0.779 | 0.7815 | |
5 | 0.8174 | 0.8103 | 0.8375 | 0.8363 | 0.8265 | 0.8385 | 0.8358 | |
I4 | 3 | 0.7457 | 0.7426 | 0.736 | 0.743 | 0.7431 | 0.7436 | 0.743 |
4 | 0.7649 | 0.7649 | 0.7617 | 0.7571 | 0.7647 | 0.7594 | 0.7652 | |
5 | 0.7911 | 0.7833 | 0.7971 | 0.8061 | 0.7973 | 0.7922 | 0.7897 | |
I5 | 3 | 0.6367 | 0.6393 | 0.6398 | 0.6384 | 0.6385 | 0.6385 | 0.6385 |
4 | 0.6998 | 0.7078 | 0.7003 | 0.7053 | 0.7088 | 0.698 | 0.7023 | |
5 | 0.7682 | 0.7601 | 0.7654 | 0.7713 | 0.76 | 0.7639 | 0.7707 | |
I6 | 3 | 0.7263 | 0.7263 | 0.7264 | 0.7264 | 0.726 | 0.7264 | 0.7264 |
4 | 0.7517 | 0.765 | 0.7666 | 0.759 | 0.7604 | 0.7251 | 0.7546 | |
5 | 0.7913 | 0.7924 | 0.7734 | 0.7946 | 0.7916 | 0.7904 | 0.7947 |
HMS | Harmony Memory Size |
HMCR | Harmony Memory Consideration Rate |
PAR | Pitch Adjustment Rate |
bw | Distance Bandwidth |
NI | Number of Improvisations |
| [1] | Sakshi, Kukreja V. Image Segmentation Techniques: Statistical, Comprehensive, Semi-Automated Analysis and an Application Perspective Analysis of Mathematical Expressions [J]. Archives of Computational Methods in Engineering, 2023, 30(1): 457-495. |
| [2] | Jiang Z, Zou F, Chen D B, et al. An ensemble multi-swarm teaching-learning-based optimization algorithm for function optimization and image segmentation [J]. Appl. Soft Comput. 2022, 130: 109653. |
| [3] | Wu, Qiang. Microscope Image Processing || Image Segmentation [J]. 2008: 159-194. |
| [4] | Abualigah L, Almotairi K H, Elaziz M A. Multilevel thresholding image segmentation using meta-heuristic optimization algorithms: comparative analysis, open challenges and new trends [J]. Applied Intelligence, 2022: 1-51. |
| [5] | Gao H, Shi Y, Pun C M, et al. An Improved Artificial Bee Colony Algorithm With its Application [J]. IEEE transactions on industrial informatics, 2019(4). |
| [6] | Otsu N. A Threshold Selection Method from Gray-Level Histograms [J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62-66. |
| [7] | Qin J, Shen X, Mei F, et al. An Otsu multi-thresholds segmentation algorithm based on improved ACO [J]. The Journal of Supercomputing, 2019, 75(2): 955-967. |
| [8] | Al-Rahlawee A T H, Rahebi J. Multilevel thresholding of images with improved Otsu thresholding by black widow optimization algorithm [J]. Multimedia Tools and Applications, 2021, 80(2–3). |
| [9] | Banerjee S, Mitra S, Uma Shankar B. Single seed delineation of brain tumor using multi-thresholding [J]. Information Sciences, 2016: 88-103. |
| [10] | Huang C, Li X, Wen Y. AN OTSU image segmentation based on fruitfly optimization algorithm [J]. AEJ - Alexandria Engineering Journal, 2020. |
| [11] | Pare S, Kumar A, Singh G K, et al. Image Segmentation Using Multilevel Thresholding: A Research Review [J]. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2020, 44(1): 1-29. |
| [12] | Shu-Liang W, He-Ji Z. Multilevel thresholding gray-scale image segmentation based on improved particle swarm optimization [J]. Journal of Computer Applications, 2012. |
| [13] | Sathya P D, Kayalvizhi R. Modified bacterial foraging algorithm based multilevel thresholding for image segmentation [J]. Engineering Applications of Artificial Intelligence, 2011, 24(4): 595-615. |
| [14] | Geem Z W, Kim J H, Loganathan G V. A New Heuristic Optimization Algorithm: Harmony Search [J]. Simulation, 2001, 2(2): 60-68. |
| [15] | Zhu Q, Tang X, Li Y, et al. An improved differential-based harmony search algorithm with linear dynamic domain [J]. Knowledge-Based Systems, 2020, 187(Jan.): 104809.1 -104809.14. |
| [16] | Kang J, Kwon S, Ryu D, et al. HASPO: Harmony Search-Based Parameter Optimization for Just-in-Time Software Defect Prediction in Maritime Software [J]. Applied Sciences, 2021, 11(5): 2002. |
| [17] | Dubey M, Kumar V, Kaur M, et al. A Systematic Review on Harmony Search Algorithm: Theory, Literature, and Applications [J]. Mathematical Problems in Engineering, 2021. |
| [18] | Cheng M Y, Prayogo D, Wu Y W, et al. A Hybrid Harmony Search algorithm for discrete sizing optimization of truss structure [J]. Automation in Construction, 2016, 69(SEP.): 21 -33. |
| [19] | Kumar V, Chhabra J K, Kumar D. Parameter adaptive harmony search algorithm for unimodal and multimodal optimization problems [J]. Journal of Computational Science, 2014, 5(2): 144-155. |
| [20] | Xiang W L, An M Q, Li Y Z, et al. An improved global-best harmony search algorithm for faster optimization [J]. Expert Systems with Applications, 2014, 41(13): 5788-5803. |
APA Style
Shu, X., Tang, X. (2024). Image Multi-threshold Segmentation Based on an Ameliorated Harmony Search Optimization Algorithm. Automation, Control and Intelligent Systems, 12(3), 60-70. https://doi.org/10.11648/j.acis.20241203.12
ACS Style
Shu, X.; Tang, X. Image Multi-threshold Segmentation Based on an Ameliorated Harmony Search Optimization Algorithm. Autom. Control Intell. Syst. 2024, 12(3), 60-70. doi: 10.11648/j.acis.20241203.12
AMA Style
Shu X, Tang X. Image Multi-threshold Segmentation Based on an Ameliorated Harmony Search Optimization Algorithm. Autom Control Intell Syst. 2024;12(3):60-70. doi: 10.11648/j.acis.20241203.12
@article{10.11648/j.acis.20241203.12,
author = {Xiuteng Shu and Xiangmeng Tang},
title = {Image Multi-threshold Segmentation Based on an Ameliorated Harmony Search Optimization Algorithm
},
journal = {Automation, Control and Intelligent Systems},
volume = {12},
number = {3},
pages = {60-70},
doi = {10.11648/j.acis.20241203.12},
url = {https://doi.org/10.11648/j.acis.20241203.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.acis.20241203.12},
abstract = {Image segmentation is the basis and premise of image processing, though traditional multi-threshold image segmentation methods are simple and effective, they suffer the problems of low accuracy and slow convergence rate. For that reason, this paper introduces the multi-threshold image segmentation scheme by combining the harmony search (HS) optimization algorithm and the maximum between-class variance (Otsu) to solve them. Firstly, to further improve the performance of the basic HS, an ameliorated harmony search (AHS) is put forward by modifying the generation method of the new harmony improvisation and introducing a convergence coefficient. Secondly, the AHS algorithm, which takes the maximum between-class variance as its objective function, namely AHS-Otsu, is applied to image multi-level threshold segmentation. Finally, six test images are selected to verify the multilevel segmentation performance of AHS-Otsu. Peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) are two commonly used metrics for evaluating the effectiveness of image segmentation, which are both used in this article. Comprehensive experimental results indicate that the AHS-Otsu does not only has fast segmentation processing speed, but also can obtain more accurate segmentation performance than others, which prove the effectiveness and potential of the AHS-Otsu algorithm in the field of image segmentation especially for the multi-threshold.
},
year = {2024}
}
TY - JOUR T1 - Image Multi-threshold Segmentation Based on an Ameliorated Harmony Search Optimization Algorithm AU - Xiuteng Shu AU - Xiangmeng Tang Y1 - 2024/08/27 PY - 2024 N1 - https://doi.org/10.11648/j.acis.20241203.12 DO - 10.11648/j.acis.20241203.12 T2 - Automation, Control and Intelligent Systems JF - Automation, Control and Intelligent Systems JO - Automation, Control and Intelligent Systems SP - 60 EP - 70 PB - Science Publishing Group SN - 2328-5591 UR - https://doi.org/10.11648/j.acis.20241203.12 AB - Image segmentation is the basis and premise of image processing, though traditional multi-threshold image segmentation methods are simple and effective, they suffer the problems of low accuracy and slow convergence rate. For that reason, this paper introduces the multi-threshold image segmentation scheme by combining the harmony search (HS) optimization algorithm and the maximum between-class variance (Otsu) to solve them. Firstly, to further improve the performance of the basic HS, an ameliorated harmony search (AHS) is put forward by modifying the generation method of the new harmony improvisation and introducing a convergence coefficient. Secondly, the AHS algorithm, which takes the maximum between-class variance as its objective function, namely AHS-Otsu, is applied to image multi-level threshold segmentation. Finally, six test images are selected to verify the multilevel segmentation performance of AHS-Otsu. Peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) are two commonly used metrics for evaluating the effectiveness of image segmentation, which are both used in this article. Comprehensive experimental results indicate that the AHS-Otsu does not only has fast segmentation processing speed, but also can obtain more accurate segmentation performance than others, which prove the effectiveness and potential of the AHS-Otsu algorithm in the field of image segmentation especially for the multi-threshold. VL - 12 IS - 3 ER -